一、梯度下降法

1.梯度下降的简单使用

神经网络的一个核心是反向传播，而反向传播的核心思想是利用梯度下降法和链式求导法则来对网络中的参数进行更新。让我们通过逻辑回归中的参数更新，简单介绍一下梯度下降法的使用。

$$
\begin{aligned}
&(1)z = W^Tx^{(i)} + b \
\end{aligned}
$$

$$
\begin{aligned}
&(2)\hat{y}=a= \sigma(z)\
\end{aligned}
$$

$$
\begin{aligned}
&(3)L(\hat{y}, y)=-ylog(\hat{y}) - (1-y)log(1-\hat{y})
\end{aligned}
$$

根据链式求导法则，可以求得以下导数公式：

$$
\begin{aligned}
&\frac{dL}{da} = -\frac{y}{a} + \frac{1-y}{1-a}\
&\frac{dL}{dz} = a - y\
&\frac{dL}{dw_i} = x_i dz\
&\frac{dL}{db} = dz\
\end{aligned}
$$

$$
(为方便书写，下文中用dw表示\frac{dL}{dw},dz表示\frac{dL}{dz},db表示\frac{dL}{db},依此类推。)
$$

上面的公式表示的并不完整，首先逻辑回归方程中的特征数量一般有多个，这就表示对应有多个w值（w1,w2,...,wn），其次就是m个样本进行梯度下降需要使用到for循环。样本数量为m，初始化：

$$
\begin{aligned}
&&J=0(代价函数) \
&&dw_1=0 \
&&dw_2=0(假设只有两个特征)\
&&db=0\
\end{aligned}
$$

梯度下降过程：

$$
\begin{aligned}
For && i=1 && to && m:\
\end{aligned}
$$

$$
\begin{aligned}
z^{(i)}=W^TX^{(i)}+b\
\end{aligned}
$$

$$
\begin{aligned}
a^{(i)}=\sigma(z^{(i)})\
\end{aligned}
$$

$$
\begin{aligned}
J=-[y^{(i)}loga^{(i)}+(1-y^{(i)})log(1-a{(i)})]\
\end{aligned}
$$

$$
\begin{aligned}
dz^{(i)}=a^{(i)}-y^{(i)}\
\end{aligned}
$$

$$
\begin{aligned}
dw_1 = dw_1 + X{^{(i)}_1}dz^{(i)}\
\end{aligned}
$$

$$
\begin{aligned}
dw_2 = dw_2 + X{^{(i)}_2}dz^{(i)}\
\end{aligned}
$$

$$
\begin{aligned}
J=\frac{j}{m}, dw_1=\frac{dw_1}{m},dw_2=\frac{dw_2}{m},db=\frac{db}{m}\
\end{aligned}
$$

$$
\begin{aligned}
w_1=w_1-\alpha dw_1, w_2=w_2-\alpha dw_2, b=b-\alpha db
\end{aligned}
$$

以上就是为一次梯度下降的全部过程，正常来说应该涉及到两层for循环：遍历m个样本和dw的更新。但是这里只给出了两个特征，不需要使用到for循环。

2.梯度下降的向量化运算

我们可以通过矩阵运算同时处理m个样本数据，避免使用for循环，加快数据的运算。假设样本数量为m，特征数量为n，则输入样本矩阵的维度为（nm），特征矩阵为（1 n）：

为了使表述更加清晰，在公式中若使用小写字母代表的单个样本或特征，大写字母代表样本全体或者特征全体。把输入样本数据向量化后，可以进行矩阵运算：

$$
\begin{aligned}
Z=W^T X+
\begin{bmatrix}
b& b & b & \cdots & b \
\end{bmatrix}
&&
A=
\begin{bmatrix}
a^{(1)}& a^{(2)} & a^{(3)} & \cdots & a^{(m)} \
\end{bmatrix}
=\sigma(Z)
\end{aligned}
$$

梯度下降参数更新公式为：

$$
\begin{aligned}
A=
\begin{bmatrix}
a^{(1)}& a^{(2)} & a^{(3)} & \cdots & a^{(m)} \
\end{bmatrix}&&
Z=
\begin{bmatrix}
z^{(1)}& z^{(2)} & z^{(3)} & \cdots & z^{(m)} \
\end{bmatrix}
&&
Y=
\begin{bmatrix}
y^{(1)}& y^{(2)} & y^{(3)} & \cdots & y^{(m)} \
\end{bmatrix}\
\end{aligned}
$$

$$
\begin{aligned}
dZ=A-Y=A=
\begin{bmatrix}
a^{(1)}-y^{(1)}& a^{(2)}-y^{(2)} & a^{(3)}-y^{(3)} & \cdots & a^{(m)}-y^{(m)} \
\end{bmatrix}
\end{aligned}
$$

$$
\begin{aligned}
db=\frac{1}{m} \sum_{i=1}^m dz^{(i)} && dW=\frac{1}{m}XdZ^T\
W=W-\alpha dW && b=b-\alpha db
\end{aligned}
$$

以上就是向量化梯度下降更新参数的整体过程，梯度下降的迭代不可避免的需要使用到for循环。python的numpy库可以很容易实现矩阵运算，在这里给出两点建议：

不要使用秩为1的矩阵。在上述公式中我们注意到W是一个一维向量，但是我们初始化时尽量不要使用:
a=numpy.random.randn(5)=>a.shape=(5,)
而是使用：
a=numpy.random.randn(5,1)=>a.shape=(5,1)
a=numpy.random.randn(1,5)=>a.shape=(1,5)

在运算过程中，计算得到的矩阵维度其实很容易推导得到的，多使用python自带的assert()时刻判断得到的矩阵维度是否正确，

二、激活函数

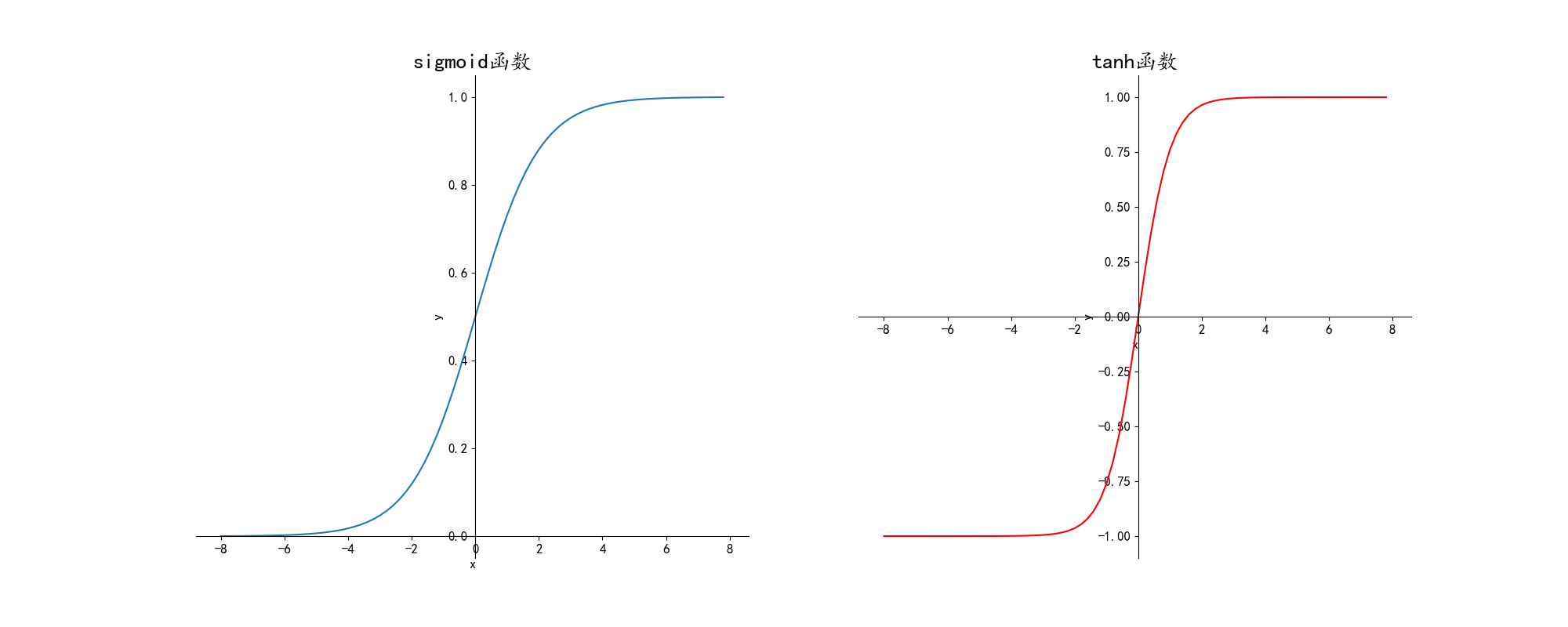
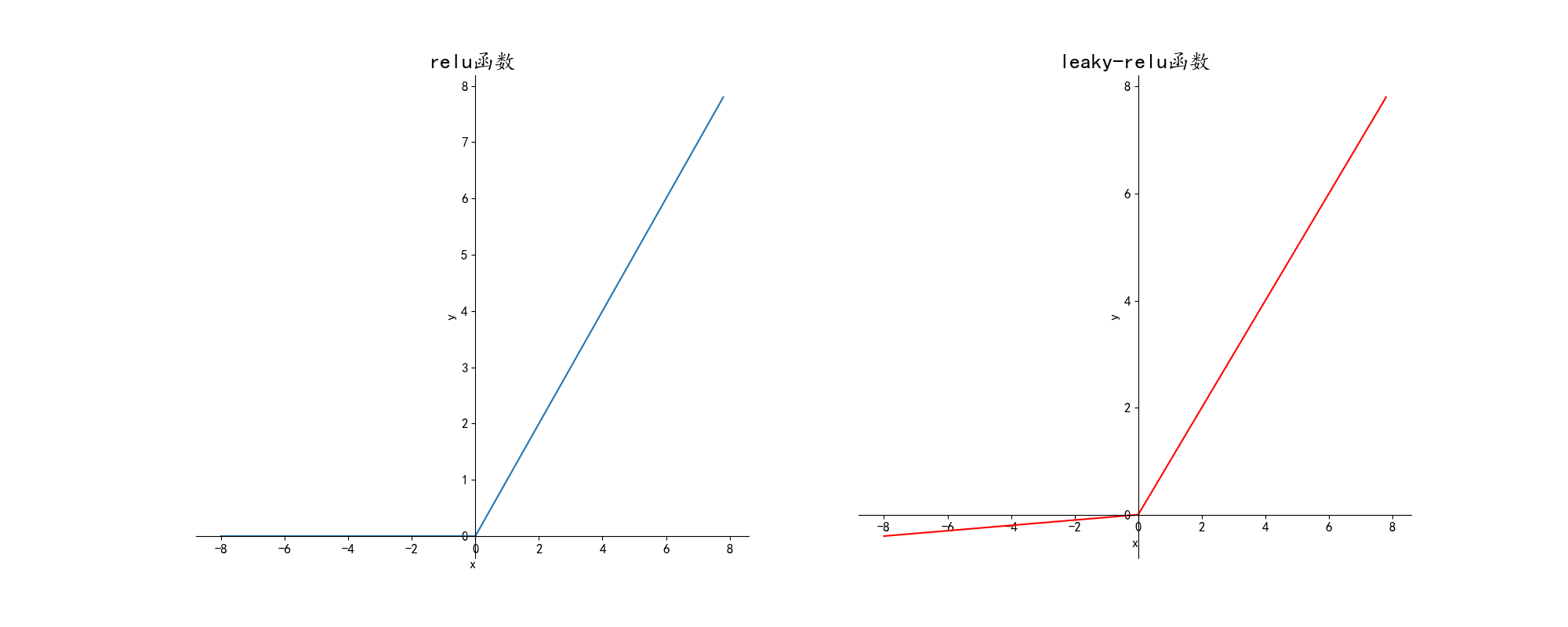
非线性激活函数通常为sigmoid，tanh，relu和leaky-relu，绘制出的图像如下：

关于激活函数的选择问题：

1.simoid:多用在二分类神经网络的输出层
2.tanh：绝大多数情况都可以使用，可以适应几乎所有情形
3.ReLU:适用范围也较为广泛
4.leaky-ReLU：效果比ReLU好，但用的比较少

为什么要使用非线性激活函数：

如果去掉非线性激活函数或者使用线性激活函数，可以很容易证明输出的y只是x的线性组合，效果特别差，这样无论隐藏层有多少层也没用。

权重参数和偏移量的初始化：

W不可初始化为0，若初始化为0，每个隐藏单元所做的处理相同，之后的每个结点计算着完全相同的函数，毫无意义。
正确的做法是，利用高斯分布的随机变量初始化W，python的numpy库提供这样的操作：W=np.random.randn((n,m))*0.01。乘上0.01系数是为了防止W过大，若是采用sigmoid或tanh，求得的斜率太低。偏移量的初始化可以为0.

三、神经网络

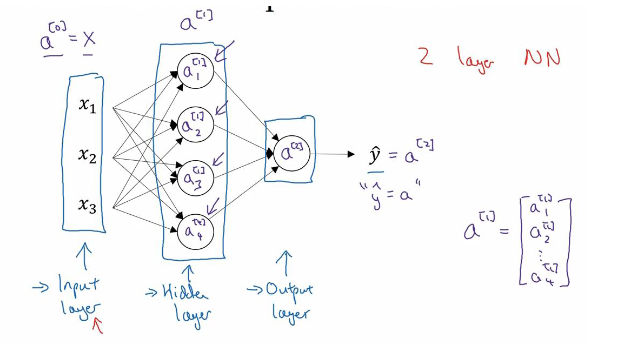
神经网络的运行过程可以简单概括为两个阶段：前向传播和反向传播。通过一个简单的例子来说明一下：

先来介绍一下神经网络的大致结构，神经网络分为输入层(Input layer)，隐藏层(Hidden layer)，输出层(Output layer)。输入层的神经元个数通常由样本数据的特征数决定，并且通常只有一层。输出层的层数和每层神经元个数根据需求自己设定，并没有一个统一的标准，上图给出的隐藏层只有一层，神经元个数为4。输出层通常也只有一层，神经元个数并不唯一，通常来说与分类数相关。

另外关于激活函数问题，输入层并未使用激活函数，每个隐藏层都有激活函数，输出层一般也有激活函数。

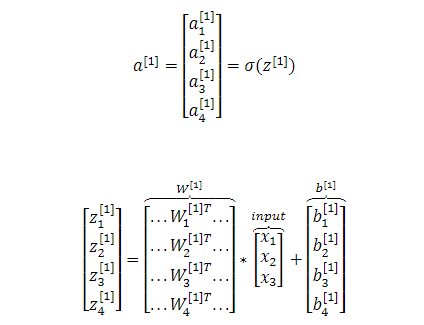
以上图简单的浅层神经网络为例，来看看怎样实行前向传播：

$$
z_1^{[1]}=w_1^{[1]T}x+b_1^{[1]},a_1^{[1]}=\sigma(z_1^{[1]})\\
z_2^{[1]}=w_2^{[1]T}x+b_2^{[1]},a_2^{[1]}=\sigma(z_2^{[1]})\\
z_3^{[1]}=w_3^{[1]T}x+b_3^{[1]},a_3^{[1]}=\sigma(z_3^{[1]})\\
z_4^{[1]}=w_4^{[1]T}x+b_4^{[1]},a_4^{[1]}=\sigma(z_4^{[1]})\\
(为方便理解，解释一下上下标的含义，例如：z_i^{[l]}表示第l层的第i个神经元线性激活结果，\\
一般认为输入层是第0层)
$$

也可以将上述运算向量化：

完整的前向传播过程为，给定输入一个样本x：

$$
a^{[0]}=x:(3,1)=(3,1)\\
z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}:(4,1)=(4,3)(3,1)+(4,1)\\
a^{[1]}=\sigma(z^{[1]}):(4,1)=(4,1)\\
z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}:(1,1)=(1,4)(4,1)+(1,1)\\
a^{[2]}=\sigma(z{[2]}):(1,1)=(1,1)\\
$$

当然也可以进行多个样本的向量化输入，这时符号需要发生一些改变，例如：

$$
a^{[l](i)}：表示第l层对第i个样本的输出值
$$

反向传播的具体过程如下，这里我直接给出公式，感兴趣的可以自己去推导一下，主要运用链式求导法则：

$$
损失函数：L(\hat{y},y)=-ylog\hat{y}-(1-y)log(1-\hat{y})\\
dz^{[2]}=A^{[2]}-Y,Y=[y^{[1]},y^{[2]},......,y^{[m]}](m为样本数)\\
dW^{[2]}=\frac{1}{m}dz^{[2]}A^{[1]T}\\
db^{[2]}\frac{1}{m}np.sum(dz^{[2]})\\
dz^{[1]}=W^{[2]T}dz^{[2]}\\
dW^{[1]}=\frac{1}{m}dz^{[1]}A^{[0]T}(A^{[0]}即是x)\\
db^{[1]}\frac{1}{m}np.sum(dz^{[1]})\\
$$

浅层神经网络可以很直观的理解，我们接下来看看深层神经网络的前向传播和反向传播。前向传播每一层的向量化公式可概括为：

$$
Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}\\
A^{[l]}=g(Z^{[l]})(g为激活函数)
$$

反向传播每一层的向量化公式可概括为：
$$
dZ^{[l]}=dA^{[l]}*g^{[l]'}(Z^{[l]})\\
dW^{[l]}=\frac{1}{m}dZ^{[l]}A^{[l-1]T}\\
db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]})\\
dA^{[l-1]}=W^{[l]T}dZ{[l]}
$$

而完整的正向和反向传播只需要根据层数，使用for循环即可。