SMO优化算法(Sequential minimal optimization)由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规划优化算法,特别针对线性SVM和数据稀疏时性能更优。在支持向量机中,我们需要优化的参数是若干个α和一个偏移量b,SMO的基本思想是每次取两个α进行优化,剩余的α固定不变,不断地迭代更新直至达到最优解。
我们先来回顾一下支持向量机中需要优化的对偶问题,以软间隔为例:
$$
\underset{\alpha}{max}\sum_{i=1}^m\alphai-\frac{1}{2}\sum{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_i^Txj\
s.t.\sum{i=1}^m\alpha_iy_i=0,0\leq\alphai\leq C
$$
上述最大化问题等价于如下最小化问题,接下来以这个最小化问题来对SMO的具体流程进行介绍:
$$
\underset{\alpha}{min}\frac{1}{2}\sum{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_i^Txj-\sum{i=1}^m\alphai,式(1)\
s.t.\sum{i=1}^m\alpha_iy_i=0,0\leq\alpha_i\leq C
$$
其KKT约束条件为:
$$
\left\{
\begin{matrix}
\alpha_i\geq0,\mu_i\geq0,\\
y_if(x_i)-1+\xi_i\geq0,\\
\alpha_i(y_if(xi)-1+\xi_i)=0,\\
\xi_i\geq0,\mu_i\xii=0
\end{matrix}
\right.
$$
以优化α1和α2为例,则需要将α3至αm固定将其看作常数,假设α1+α2=c,式(1)的后半部分可拆分成:
$$
\sum{i=1}^m\alpha_i=\alpha_1+\alpha2+\sum{i=1}^m\alpha_i=\alpha_1+\alpha_2+c_1,式(2)\\
(其中c_1为常数)
$$
式(1)的前半部分可以拆分成三段进行计算:
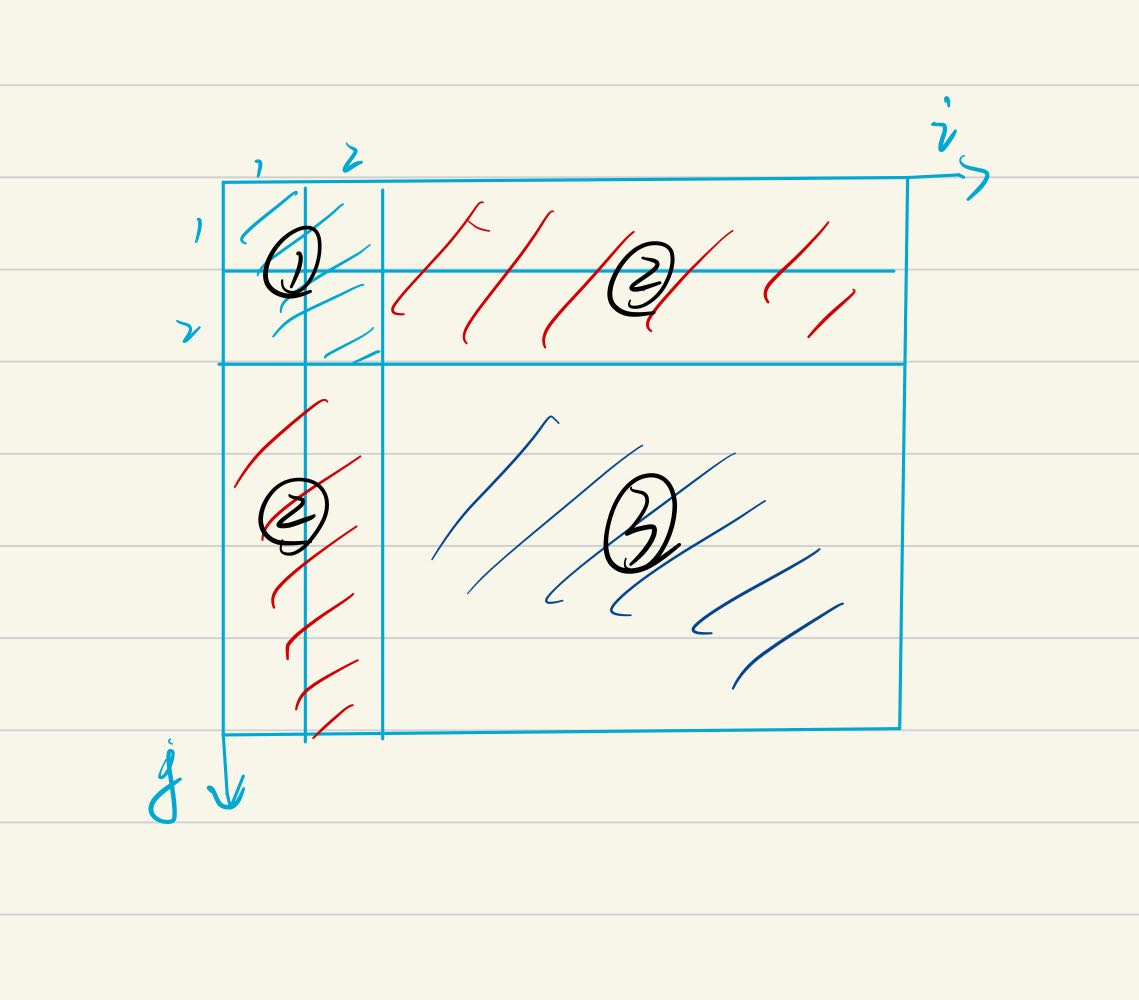
①的计算结果为:
$$
\frac{1}{2}\alpha_1\alpha_1y_1y1K{11}+\frac{1}{2}\alpha_1\alpha_2y_1y2K{12}+\frac{1}{2}\alpha_2\alpha_1y_2y1K{21}+\frac{1}{2}\alpha_2\alpha_2y_2y2K{22}\\
=>\frac{1}{2}\alpha_1^2K11+\frac{1}{2}\alpha2^2K{22}+\alpha_1\alpha_2y_1y2K{12},式(3)\\
(其中K_{ij}=x_i^Txj)
$$
②的计算结果为:
$$
\frac{1}{2}\sum{j=3}^{m}\alpha_1\alpha_jy_1yjK{1j}+\frac{1}{2}\sum_{j=3}^m\alpha_2\alpha_jy_2yjK{2j}+\frac{1}{2}\sum_{i=3}^m\alpha_i\alpha_1y_iy1K{i1}+\frac{1}{2}\sum_{i=3}^m\alpha_i\alpha_2y_iy2K{i2}\\
=>\alpha_1y1\sum{i=3}^m\alpha_iyiK{1i}+\alpha_2y2\sum{i=3}^m\alpha_iyiK{2i},式(4)
$$
③的计算结果为一个常数:
$$
c2=\frac{1}{2}\sum{i=3}^m\sum_{j=3}^m\alpha_i\alpha_jy_iyjK{ij},式(5)
$$
综合式(2),(3),(4),(5),式(1)转化为:
$$
\underset{\alpha}{min}\frac{1}{2}\alpha1^2K{11}+\frac{1}{2}\alpha2^2K{22}+\alpha_1\alpha_2y_1y2K{12}+\alpha_1y1\sum{i=3}^m\alpha_iyiK{1i}+\alpha_2y2\sum{i=3}^m\alpha_iyiK{2i}-(\alpha_1+\alpha_2)+c,式(6)\\
(c为常数项)
$$
接下来用α2表示α1:
$$
假设\alpha_1y_1+\alpha_2y_2=C\\
可得\alpha_1=(C-\alpha_2y_2)y_1\\
(|y_1|=|y_2|=1)
$$
代入到式(6)中可得:
$$
\underset{\alpha}{min}\frac{1}{2}[(C-\alpha_2y2)]^2K{11}+\frac{1}{2}\alpha2^2K{22}+(C-\alpha_2y_2)\alpha_2y2K{12}+(C-\alpha_2y2)\sum{i=3}^m\alpha_iyiK{1i}\\
+\alpha_2y2\sum{i=3}^m\alpha_iyiK{2i}-(C-\alpha_2y_2)y_1-\alpha2+c,式(7)
$$
现在优化目标中只有α2这一个变量,对其求偏导得:
$$
(K{11}+K{22}-2K{12})\alpha2-K{11}Cy2+K{12}Cy_2+y_1y_2-1-y2\sum{i=3}^m\alpha_iyiK{1i}+y2\sum{i=3}\alpha_iyiK{2i},式(8)
$$
已知:
$$
\left\{
\begin{matrix}
\alpha_1^{old}y_1+\alpha_2^{old}y2=C\\
\sum{i=3}^m\alpha_iyiK{1i}=f(x_1)-y_1\alpha1K{11}-y_2\alpha2K{12}-b\\
\sum_{i=3}^m\alpha_iyiK{2i}=f(x_2)-y_1\alpha1K{21}-y_2\alpha2K{22}-b
\end{matrix}
\right.
$$
将上述已知条件代入到式(8)中,并令导数为0可得:
$$
(K{11}+K{22}-2K_{12})\alpha2^{new}=(K{11}+K{22}-2K{12})\alpha_2^{old}+y_2[(f(x_1)-y_1)-(f(x_2)-y_2)]
$$
记:
$$
\eta=K{11}+K{22}-2K_{12}
$$
若η小于等于0则退出本次优化,反之就更新α2的值:
$$
\alpha_2^{new}=\alpha_2^{old}+\frac{y_2\{[f(x_1)-y_1]-[f(x_2)-y_2]\}}{\eta}
$$
α1的更新公式为:
$$
需要保证:\sum_{i=1}^m\alpha_iy_i=0,则\alpha_1^{new}y_1+\alpha_2^{new}y_2=\alpha_1^{old}y_1+\alpha_2^{old}y_2\\
可得:\alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new})
$$
常数b的更新公式为:
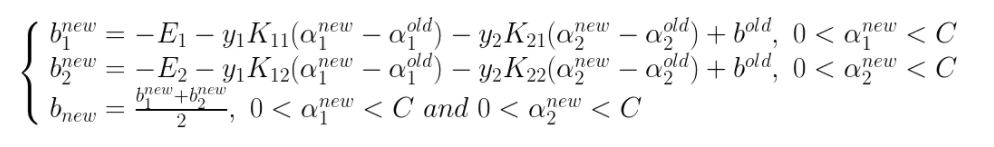
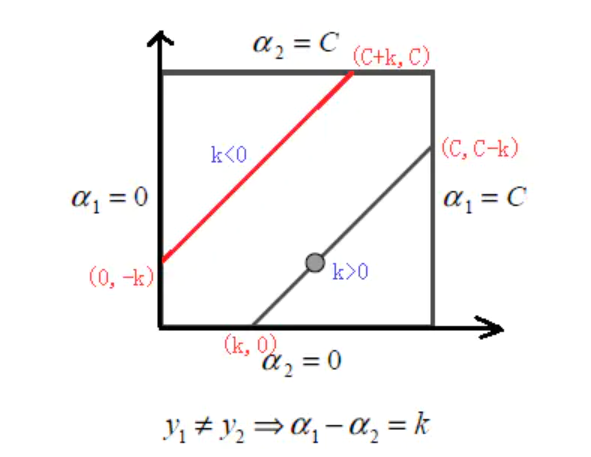
除此之外,我们还需要考虑α1和α2的取值范围,设α1y1+α2y2=k,当y1!=y2时,α1-α2=k:
$$
\left\{
\begin{matrix}
low=max(0,-k)\\
high=min(C,C-k)
\end{matrix}
\right.
$$
当y1=y2时,α1+α2=k:
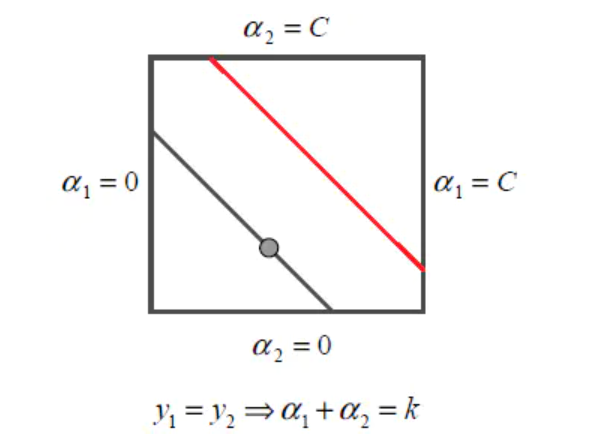
此时α2的取值范围为:
$$
\left\{
\begin{matrix}
low=max(0,k-C)\\
high=min(C,k)
\end{matrix}
\right.
$$
α2的上下界取值规律为:
$$
\left\{
\begin{matrix}
low=max(0,-k),high=min(C,C-k),y_1\neq y_2\\
low=max(0,k-C),high=min(C,k),y_1=y_2
\end{matrix}
\right.
$$